Trang chủ Đề thi Lớp 11 Toán 12991

Trắc nghiệm Toán 11 Bài 4: Trắc nghiệm vi phân của hàm số có đáp án (Mới nhất)

Chương 5: Đạo hàm
Bài 4: Vi phân
Lớp 11;Toán

Bộ sưu tập: TOÁN 11

Số câu hỏi: 34 câuSố mã đề: 1 đềThời gian: 1 giờ

168,969 lượt xem 12,991 lượt làm bài

Bạn chưa làm đề thi này!

Xem trước nội dung
Câu 1: 1 điểm

Cho hàm số \(y = f\left( x \right) = {\left( {x - 1} \right)^2}\). Biểu thức nào sau đây chỉ vi phân của hàm số\(f\left( x \right)\)?

A.  
\({\rm{d}}y = 2\left( {x - 1} \right){\rm{d}}x\).
B.  
\({\rm{d}}y = {\left( {x - 1} \right)^2}{\rm{d}}x\).
C.  
\({\rm{d}}y = 2\left( {x - 1} \right)\).
D.  
\({\rm{d}}y = 2\left( {x - 1} \right){\rm{d}}x\).
Câu 2: 1 điểm

Tìm vi phân của các hàm số \(y = {x^3} + 2{x^2}\)

A.  
\(dy = (3{x^2} - 4x)dx\)
B.  
\(dy = (3{x^2} + x)dx\)
C.  
\(dy = (3{x^2} + 2x)dx\)
D.  
\(dy = (3{x^2} + 4x)dx\)
Câu 3: 1 điểm

Tìm vi phân của các hàm số \(y = \sqrt {3x + 2} \)

A.  
\(dy = \frac{3}{{\sqrt {3x + 2} }}dx\)
B.  
\(dy = \frac{1}{{2\sqrt {3x + 2} }}dx\)
C.  
\(dy = \frac{1}{{\sqrt {3x + 2} }}dx\)
D.  
\(dy = \frac{3}{{2\sqrt {3x + 2} }}dx\)
Câu 4: 1 điểm

Cho hàm số \(y = {x^3} - 9{x^2} + 12x - 5\). Vi phân của hàm số là:

A.  
\({\rm{d}}y = \left( {3{x^2} - 18x + 12} \right){\rm{d}}x\).
B.  
\({\rm{d}}y = \left( { - 3{x^2} - 18x + 12} \right){\rm{d}}x\).
C.  
\({\rm{d}}y = - \left( {3{x^2} - 18x + 12} \right){\rm{d}}x\).
D.  
\({\rm{d}}y = \left( { - 3{x^2} + 18x - 12} \right){\rm{d}}x\).
Câu 5: 1 điểm

Tìm vi phân của các hàm số \(y = {(3x + 1)^{10}}\)

A.  
\(dy = 10{(3x + 1)^9}dx\)
B.  
\(dy = 30{(3x + 1)^{10}}dx\)
C.  
\(dy = 9{(3x + 1)^{10}}dx\)
D.  
\(dy = 30{(3x + 1)^9}dx\)
Câu 6: 1 điểm

Tìm vi phân của các hàm số \(y = \sin 2x + {\sin ^3}x\)

A.  
\(dy = \left( {\cos 2x + 3{{\sin }^2}x\cos x} \right)dx\)
B.  
\(dy = \left( {2\cos 2x + 3{{\sin }^2}x\cos x} \right)dx\)
C.  
\(dy = \left( {2\cos 2x + {{\sin }^2}x\cos x} \right)dx\)
D.  
\(dy = \left( {\cos 2x + {{\sin }^2}x\cos x} \right)dx\)
Câu 7: 1 điểm

Tìm vi phân của các hàm số \(y = \tan 2x\)

A.  
\(dy = (1 + {\tan ^2}2x)dx\)
B.  
\(dy = (1 - {\tan ^2}2x)dx\)
C.  
\(dy = 2(1 - {\tan ^2}2x)dx\)
D.  
\(dy = 2(1 + {\tan ^2}2x)dx\)
Câu 8: 1 điểm

Tìm vi phân của các hàm số \(y = \sqrt[3]{{x + 1}}\)

A.  
\(dy = \frac{1}{{\sqrt[3]{{{{(x + 1)}^2}}}}}dx\)
B.  
\(dy = \frac{3}{{\sqrt[3]{{{{(x + 1)}^2}}}}}dx\)
C.  
\(dy = \frac{2}{{\sqrt[3]{{{{(x + 1)}^2}}}}}dx\)
D.  
\(dy = \frac{1}{{3\sqrt[3]{{{{(x + 1)}^2}}}}}dx\)
Câu 9: 1 điểm

Xét hàm số \(y = f\left( x \right) = \sqrt {1 + {{\cos }^2}2x} \). Chọn câu đúng:

A.  
\({\rm{d}}f(x) = \frac{{ - \sin 4x}}{{2\sqrt {1 + {{\cos }^2}2x} }}{\rm{d}}x\).
B.  
\({\rm{d}}f(x) = \frac{{ - \sin 4x}}{{\sqrt {1 + {{\cos }^2}2x} }}{\rm{d}}x\).
C.  
\({\rm{d}}f(x) = \frac{{\cos 2x}}{{\sqrt {1 + {{\cos }^2}2x} }}{\rm{d}}x\).
D.  
\({\rm{d}}f(x) = \frac{{ - \sin 2x}}{{2\sqrt {1 + {{\cos }^2}2x} }}{\rm{d}}x\).
Câu 10: 1 điểm

Cho hàm số\(y = {x^3} - 5x + 6\) . Vi phân của hàm số là:

A.  
\({\rm{d}}y = \left( {3{x^2} - 5} \right){\rm{d}}x\).
B.  
\({\rm{d}}y = - \left( {3{x^2} - 5} \right){\rm{d}}x\).
C.  
\({\rm{d}}y = \left( {3{x^2} + 5} \right){\rm{d}}x\).
D.  
\({\rm{d}}y = \left( {3{x^2} - 5} \right){\rm{d}}x\).
Câu 11: 1 điểm

Cho hàm số \(y = \frac{1}{{3{x^3}}}\). Vi phân của hàm số là:

A.  
\({\rm{d}}y = \frac{1}{4}{\rm{d}}x\).
B.  
\({\rm{d}}y = \frac{1}{{{x^4}}}{\rm{d}}x\).
C.  
\({\rm{d}}y = - \frac{1}{{{x^4}}}{\rm{d}}x\).
D.  
\({\rm{d}}y = {x^4}{\rm{d}}x\).
Câu 12: 1 điểm

Cho hàm số \(y = \frac{{x + 2}}{{x - 1}}\). Vi phân của hàm số là:

A.  
\({\rm{d}}y = \frac{{{\rm{d}}x}}{{{{\left( {x - 1} \right)}^2}}}\).
B.  
\({\rm{d}}y = \frac{{3{\rm{d}}x}}{{{{\left( {x - 1} \right)}^2}}}\).
C.  
\({\rm{d}}y = \frac{{ - 3{\rm{d}}x}}{{{{\left( {x - 1} \right)}^2}}}\).
D.  
\({\rm{d}}y = - \frac{{{\rm{d}}x}}{{{{\left( {x - 1} \right)}^2}}}\).
Câu 13: 1 điểm

Cho hàm số \(y = \frac{{{x^2} + x + 1}}{{x - 1}}\). Vi phân của hàm số là:

A.  
\({\rm{d}}y = - \frac{{{x^2} - 2x - 2}}{{{{(x - 1)}^2}}}{\rm{d}}x\).
B.  
\({\rm{d}}y = \frac{{2x + 1}}{{{{(x - 1)}^2}}}{\rm{d}}x\).
C.  
\({\rm{d}}y = - \frac{{2x + 1}}{{{{(x - 1)}^2}}}{\rm{d}}x\).
D.  
\({\rm{d}}y = \frac{{{x^2} - 2x - 2}}{{{{(x - 1)}^2}}}{\rm{d}}x\).
Câu 14: 1 điểm

Cho hàm số \(y = \sin x - 3\cos x\). Vi phân của hàm số là:

A.  
\({\rm{d}}y = \left( { - \cos x + 3\sin x} \right){\rm{d}}x\).
B.  
\({\rm{d}}y = \left( { - \cos x - 3\sin x} \right){\rm{d}}x\).
C.  
\({\rm{d}}y = \left( {\cos x + 3\sin x} \right){\rm{d}}x\).
D.  
\({\rm{d}}y = - \left( {\cos x + 3\sin x} \right){\rm{d}}x\).
Câu 15: 1 điểm

Cho hàm số \[y = {\sin ^2}x\]. Vi phân của hàm số là:

A.  
\[{\rm{d}}y = -\sin 2x\,{\rm{d}}x\].
B.  
\[{\rm{d}}y = \sin 2x\,{\rm{d}}x\].
C.  
\[{\rm{d}}y = \sin x\,{\rm{d}}x\].
D.  
\[{\rm{d}}y = {\rm{2cos}}x\,{\rm{d}}x\].
Câu 16: 1 điểm

Vi phân của hàm số \[y = \frac{{\tan \sqrt x }}{{\sqrt x }}\]là:

A.  
\[{\rm{d}}y = \frac{{2\sqrt x }}{{4x\sqrt x {{\cos }^2}\sqrt x }}{\rm{d}}x\].
B.  
\[{\rm{d}}y = \frac{{\sin (2\sqrt x )}}{{4x\sqrt x {{\cos }^2}\sqrt x }}{\rm{d}}x\].
C.  
\[{\rm{d}}y = \frac{{2\sqrt x - \sin (2\sqrt x )}}{{4x\sqrt x {{\cos }^2}\sqrt x }}{\rm{d}}x\].
D.  
\[{\rm{d}}y = - \frac{{2\sqrt x - \sin (2\sqrt x )}}{{4x\sqrt x {{\cos }^2}\sqrt x }}{\rm{d}}x\].
Câu 17: 1 điểm

Hàm số \[y = x\sin x + \cos x\] có vi phân là:

A.  
\[{\rm{d}}y = \left( {x\cos x-\sin x} \right){\rm{d}}x\].
B.  
\[{\rm{d}}y = \left( {x\cos x} \right){\rm{d}}x\].
C.  
\[{\rm{d}}y = \left( {\cos x-\sin x} \right){\rm{d}}x\]..
D.  
\[{\rm{d}}y = \left( {x\sin x} \right){\rm{d}}x\].
Câu 18: 1 điểm

Hàm số \(y{\rm{ }} = \frac{x}{{{x^2} + 1}}\). Có vi phân là:

A.  
\[dy = \frac{{1 - {x^2}}}{{{{({x^2} + 1)}^2}}}dx\]
B.  
\[dy = \frac{{2x}}{{({x^2} + 1)}}dx\]
C.  
\[dy = \frac{{1 - {x^2}}}{{({x^2} + 1)}}dx\]
D.  
\[dy = \frac{1}{{{{({x^2} + 1)}^2}}}dx\]
Câu 19: 1 điểm

Cho hàm số Hình ảnh . Biểu thức nào sau đây là vi phân của hàm số đã cho?

A.  
A. Media VietJack .
B.  
B. Media VietJack .
C.  
C. Media VietJack . 
D.  
D. Media VietJack .
Câu 20: 1 điểm

Vi phân của hàm số Hình ảnh tại điểm x = 2, ứng với Hình ảnh là:

A.  
-0,07.
B.  
10.
C.  
1,1.
D.  
-0,4 .
Câu 21: 1 điểm

Vi phân của y = cot(2017x) là:

A.  
A. Media VietJack
B.  
B.  Media VietJack
C.  
 Media VietJack
D.  
D.  Media VietJack
Câu 22: 1 điểm

Cho hàm số y = Hình ảnh. Vi phân của hàm số là:

A.  
A. Media VietJack
B.  
B. Media VietJack
C.  
C. Media VietJack
D.  
D. Media VietJack
Câu 23: 1 điểm

Cho hàm số Hình ảnh . Vi phân của hàm số tại Hình ảnh là:

A.  
Media VietJack
B.  
B.  Media VietJack 
C.  
C. Media VietJack
D.  
D.  Media VietJack
Câu 24: 1 điểm

Vi phân của y = tan5x là :

A.  
A. Media VietJack
B.  
B. Media VietJack
C.  
C. Media VietJack
D.  
D. Media VietJack
Câu 25: 1 điểm

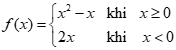Hàm số Hình ảnh. Biểu thức 0,01f'(0,01) là số nào?

A.  
9.
B.  
-9.
C.  
90.
D.  
-90.
Câu 26: 1 điểm

Cho hàm số Hình ảnh.Vi phân của hàm số là:

A.  
A. Media VietJack.
B.  
B. Media VietJack.
C.  
C. Media VietJack.
D.  
D. Media VietJack.
Câu 27: 1 điểm

Cho hàm số Hình ảnh. Kết quả nào dưới đây đúng?

A.  
A. Media VietJack.
B.  
B. Media VietJack.
C.  
C. Media VietJack.
D.  
D. Media VietJack.
Câu 28: 1 điểm

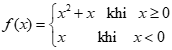Cho hàm số Hình ảnh . Vi phân của hàm số là:

A.  
Media VietJack
B.  
Media VietJack
C.  
C. Media VietJack
D.  
Media VietJack
Câu 29: 1 điểm

Cho hàm số Hình ảnh . Khẳng định nào dưới đây là sai?

A.  
f'(0+) = 1
B.  
f'(0-) = 1 .
C.  
d f(0) = dx
D.  
Hàm số không có vi phân tại x = 0 .
Câu 30: 1 điểm

Cho hàm số Hình ảnh. Chọn kết quả đúng:

A.  
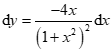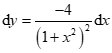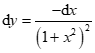A. Media VietJack.
B.  
B. Media VietJack.
C.  
C. Media VietJack. 
D.  
D. Media VietJack.
Câu 31: 1 điểm

Cho hàm số Hình ảnh. Vi phân của hàm số là:

A.  
A. Media VietJack.
B.  
B. Media VietJack.
C.  
C. Media VietJack.
D.  
D. Media VietJack.
Câu 32: 1 điểm

Vi phân của hàm số Hình ảnh là :

A.  
A. Media VietJack.
B.  
B. Media VietJack.
C.  
C. Media VietJack.
D.  
D. Media VietJack.
Câu 33: 1 điểm

Cho hàm số Hình ảnh. Vi phân của hàm số là:

A.  
A. Media VietJack.
B.  
B. Media VietJack.
C.  
C. Media VietJack.
D.  
D. Media VietJack.
Câu 34: 1 điểm

Cho hàm số Hình ảnh. Khi đó

A.  
A. Media VietJack.
B.  
B. Media VietJack.
C.  
C. Media VietJack.
D.  
D. Media VietJack.

 

Tuyển tập bộ đề
TOÁN 11

1,591 xem