Trắc nghiệm Giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đáp án (Vận dụng)

Có bao nhiêu số nguyên m thuộc đoạn [-20;20] để giá trị lớn nhất của hàm số $y=\frac{x+m+6}{x-m}$trên đoạn [1;3] là số dương?

Cho hàm số y=f(x) trên đoạn [-2;4] như hình vẽ. Gọi S là tập chứa các giá trị của m để hàm số $y={\left(f\left(2-x\right)+m\right)}^2$có giá trị lớn nhất trên đoạn [-2;4] bằng 49. Tổng các phần tử của tập S bằng

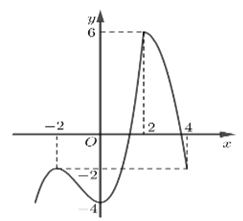
Cho hàm số bậc bốn y=f(x) có đồ thị như hình vẽ bên

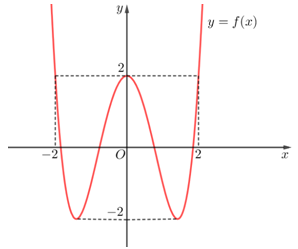
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn $\left.0;20\right]$sao cho giá trị nhỏ nhất của hàm số $g\left(x\right)=\left.\left.2f\left(x\right)+m+4\right|-f\left(x\right)-3\right|$trên đoạn $\left.-2;2\right]$không bé hơn 1?

Có bao nhiêu giá trị của m để giá trị nhỏ nhất của hàm số $y=\left.e^{2x}-4e^x+m\right|$trên đoạn $\left.0;\ln 4\right]$bằng 6.

Một người bán gạo muốn đóng một thùng tôn đựng gạo thể tích không đổi bằng $V=5m^3$, thùng tôn hình hộp chữ nhật có đáy là hình vuông, không nắp. Trên thị trường, giá tôn làm đáy thùng là $10\$/1m^2$, giá tôn làm mặt xung quanh của thùng là $8\$/1m^2$. Hỏi người bán gạo đó đóng thùng đựng gạo với cạnh đáy bằng bao nhiêu sao cho chi phí mua nguyên liệu là nhỏ nhất?

Từ một miếng tôn dạng nửa hình tròn có bán kính R=4 người ta muốn cắt ra một hình chữ nhật. Hỏi diện tích lớn nhất của hình chữ nhật có thể cắt được từ miếng tôn là

Diện tích lớn nhất của hình chữ nhật nội tiếp hình tròn bán kính bằng 10cm là:

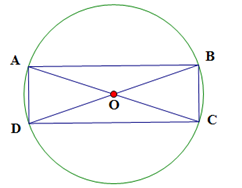
Một mảnh vườn hình chữ nhật có diện tích $961m^2$, người ta muốn mở rộng thêm bốn phần đất sao cho tạo thành hình tròn ngoại tiếp mảnh vườn (xem hình minh họa). Tính diện tích nhỏ nhất $S_{\min }$của bốn phần đất được mở rộng.

Cho tam giác đều ABC cạnh a. Người ta dựng một hình chữ nhật MNPQ có cạnh MN nằm trên BC hai đỉnh P và Q theo thứ tự nằm trên cạnh AC và AB của tam giác. Giá trị lớn nhất của diện tích hình chữ nhật đó là

Giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số $f\left(x\right)=\left.x^3-3x+m\right|$trên đoạn $\left.0;3\right]$đạt giá trị nhỏ nhất. Khi đó kết luận nào sau đây là đúng?