Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán Chủ đề 8: Hàm số luỹ thừa, hàm số mũ và hàm số logarit. Phương trình, bất phương trình mũ và logarit có đáp án
Bộ câu hỏi trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán, chủ đề Hàm số lũy thừa, hàm số mũ và logarit. Tài liệu bao gồm các dạng bài về phương trình và bất phương trình mũ, logarit, kèm đáp án chi tiết để hỗ trợ học sinh ôn tập và luyện thi hiệu quả.
Từ khoá: Toán học hàm số lũy thừa logarit phương trình mũ bất phương trình ôn thi tốt nghiệp năm 2022 đề thi có đáp án
Bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết📘 Tuyển Tập Đề Thi Tham Khảo Các Môn THPT Quốc Gia 2025 🎯
Số câu hỏi: 100 câuSố mã đề: 5 đềThời gian: 1 giờ
183,294 lượt xem 14,090 lượt làm bài
Bạn chưa làm Đề số 1!
Xem trước nội dung
Câu 1: 1 điểm
Tập hợp các căn bậc hai của 25 là
A.
\(\{ 5\} .\)
B.
\(\{ - 5\} .\)
C.
\(\{ - 5;5\} .\)
D.
\(\{ 625\} .\)
Câu 2: 1 điểm
Cho \({\rm{a}},{\rm{b}}\) là các số dương khác 1. Phát biểu nào sau đây là đúng?
A.
\(a = {a^{{{\log }_a}b}}.\)
B.
\({\rm{b}} = {{\rm{a}}^{{{\log }_{\rm{a}}}{\rm{b}}}}.\)
C.
\({\rm{b}} = {{\rm{b}}^{{{\log }_a}\;{\rm{b}}}}.\)
D.
\({\rm{a}} = {{\rm{a}}^{{{\log }_b}{\rm{a}}}}.\)
Câu 3: 1 điểm
Số 16 có bao nhiêu căn bậc hai?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 4: 1 điểm
Cho \({\rm{a}} > 0,{\rm{a}} e 1\) và \({\rm{x}},{\rm{y}}\) là hai số dương. Phát biểu nào sau đây là đúng?
A.
A. \({\log _a}(xy) = {\log _a}x \cdot {\log _a}y.\)
B.
B. \({\log _a}(xy) = \frac{{{{\log }_a}x}}{{{{\log }_a}y}}.\)
C.
C. \({\log _{\rm{a}}}({\rm{xy}}) = {\log _{\rm{a}}}{\rm{x}} + {\log _{\rm{a}}}{\rm{y}}.\)
D.
D. \({\log _a}(xy) = \frac{{{{\log }_a}y}}{{{{\log }_a}x}}.\)
Câu 5: 1 điểm
Cho \({\rm{a}} > 0,{\rm{a}} e 1\) và x, y là hai số dương. Phát biểu nào sau đây là đúng?
A.
\({\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y.\)
B.
\({\log _a}\frac{x}{y} = {\log _a}x \cdot {\log _a}y.\)
C.
\({\log _a}\frac{x}{y} = \frac{{{{\log }_a}x}}{{{{\log }_a}y}}.\)
D.
\({\log _a}\frac{x}{y} = {\log _a}x + {\log _a}y.\)
Câu 6: 1 điểm
Cho
và
Phát biểu nào sau đây là đúng?
A.
\({\log _a}{x^\alpha } = \frac{1}{\alpha }{\log _a}x.\)
B.
\({\log _{\rm{a}}}{{\rm{x}}^\alpha } = {\log _{\rm{a}}}(\alpha {\rm{x}}).\)
C.
\({\log _{\rm{a}}}{{\rm{x}}^\alpha } = {\log _{\rm{a}}}\frac{{\rm{x}}}{\alpha }.\)
D.
\({\log _{\rm{a}}}{{\rm{x}}^\alpha } = \alpha {\log _{\rm{a}}}{\rm{x}}.\)
Câu 7: 1 điểm
Cho \({\rm{a}} > 0,{\rm{a}} e 1\) và x, y là hai số dương. Phát biểu nào sau đây là đúng?
A.
\({\left( {{{\rm{a}}^{\rm{x}}}} \right)^{\rm{y}}} = {{\rm{a}}^{{\rm{xy}}}}.\)
B.
\({\left( {{a^x}} \right)^y} = {a^{x + y}}.\)
C.
\({\left( {{a^x}} \right)^y} = {a^{x - y}}.\)
D.
\({\left( {{a^x}} \right)^y} = {a^{\frac{x}{y}}}.\)
Câu 8: 1 điểm
Cho \({\rm{a}} > 0,{\rm{a}} e 1\) và n là số nguyên dương. Phát biểu nào sau đây là đúng?
A.
\({{\rm{a}}^{ - {\rm{n}}}} = - {{\rm{a}}^{\rm{n}}}.\)
B.
\({{\rm{a}}^{ - {\rm{n}}}} = \frac{1}{{{{\rm{a}}^{\rm{n}}}}}.\)
C.
\({{\rm{a}}^{ - {\rm{n}}}} = \frac{{ - 1}}{{{{\rm{a}}^{\rm{n}}}}}.\)
D.
\({a^{ - {\rm{n}}}} = {{\rm{a}}^{\rm{n}}}.\)
Câu 9: 1 điểm
Cho \({\rm{a}} > 0,{\rm{a}} e 1\) và n là số nguyên dương lớn hơn 1. Phát biểu nào sau đây là đúng?
A.
\(\sqrt[n]{a} = {a^{\frac{1}{n}}}.\)
B.
\(\sqrt[n]{a} = - {a^{\frac{1}{n}}}.\)
C.
\(\sqrt[n]{{\rm{a}}} = \frac{{\rm{a}}}{{\rm{n}}}.\)
D.
\(\sqrt[n]{{\rm{a}}} = \frac{1}{{{{\rm{a}}^{\frac{1}{n}}}}}.\)
Câu 10: 1 điểm
Cho \({\rm{a}} = {\log _2}3,\;{\rm{b}} = {\log _5}3.\) Biểu thức \({\log _{10}}3\) bằng
A.
\(\frac{{{\rm{ab}}}}{{{\rm{a}} + {\rm{b}}}}.\)
B.
\(\frac{1}{{\rm{a}}} + \frac{1}{{\;{\rm{b}}}}.\)
C.
\(\frac{1}{{{\rm{ab}}}}.\)
D.
ab.
Câu 11: 1 điểm
Phát biểu nào sau đây là đúng?
A.
\({\log _2}{x^2} = 2{\log _2}x,\forall x e 0.\)
B.
\({\log _2}{{\rm{x}}^2} = \frac{1}{2}{\log _2}{\rm{x}},\forall {\rm{x}} e 0.\)
C.
\({\log _2}{x^2} = {2^2}{\log _2}|x|,\forall x e 0.\)
D.
\({\log _2}{x^2} = 2{\log _2}|x|,\forall x e 0.\)
Câu 12: 1 điểm
Cho a là số dương khác \(1;{\rm{m}},{\rm{n}},{\rm{p}},{\rm{q}}\) là các số nguyên dương lớn hơn 1. Phát biểu nào sau đây là đúng?
A.
\({\log _{\sqrt[m]{{{a^a}}}}}\sqrt[p]{{{a^q}}} = \frac{m}{n} \cdot \frac{q}{p}.\)
B.
\({\log _{\sqrt[m]{{{a^n}}}}}\sqrt[p]{{{a^q}}} = \frac{n}{m} \cdot \frac{q}{p}.\)
C.
\({\log _{\sqrt[m]{{{a^a}}}}}\sqrt[p]{{{a^q}}} = \frac{m}{n} \cdot \frac{p}{q}.\)
D.
\({\log _{\sqrt[m]{{{a^n}}}}}\sqrt[p]{{{a^q}}} = \frac{n}{m} \cdot \frac{p}{q}.\)
Câu 13: 1 điểm
Cho \({\rm{a}},{\rm{b}}\) là hai số thực dương thoả mãn \({{\rm{a}}^2} + {{\rm{b}}^2} = 98{\rm{ab}}.\) Phát biểu nào sau đây là đúng?
A.
\(2{\log _2}({\rm{a}} + {\rm{b}}) = {\log _2}{\rm{a}} + {\log _2}\;{\rm{b}}.\)
B.
\({\log _2}\frac{{a + b}}{2} = {\log _2}a + {\log _2}b.\)
C.
\(2{\log _2}\frac{{a + b}}{{10}} = {\log _2}a + {\log _2}\;{\rm{b}}.\)
D.
\({\log _2}\frac{{a + b}}{{10}} = 2\left( {{{\log }_2}a + {{\log }_2}b} \right)\)
Câu 14: 1 điểm
Biết \({\log _2}3 = {\rm{a}}\) và \({\log _2}5 = {\rm{b}}.\) Kết quả tính \({\log _5}360\) theo a và b là
A.
\(\frac{{3{\rm{a}} + {\rm{b}} + 2}}{{\;{\rm{b}}}}.\)
B.
\(\frac{{2{\rm{a}} + {\rm{b}} + 3}}{{\;{\rm{b}}}}.\)
C.
\({\rm{b}}(2{\rm{a}} + {\rm{b}} + 3).\)
D.
\({\rm{b}}(3{\rm{a}} + {\rm{b}} + 2).\)
Câu 15: 1 điểm
Biết \({\log _8}3 = {\rm{a}}\) và \({\log _3}5 = {\rm{b}}.\) Kết quả tính \({\log _{10}}3\) theo a và b là
A.
\(3{\rm{a}} + {\rm{b}}.\)
B.
ab.
C.
\(\frac{1}{{a + 3b}}.\)
D.
\(\frac{{3{\rm{a}}}}{{1 + 3{\rm{ab}}}}.\)
Câu 16: 1 điểm
Biết \({\rm{a}} = {\log _2}3\) và \({\rm{b}} = {\log _2}5.\) Giá trị của biểu thức \({\log _{15}}45\) bằng
A.
\(\frac{{{\rm{a}} + {\rm{b}}}}{{2{\rm{a}} + {\rm{b}}}}.\)
B.
\(\frac{{a + 2b}}{{a + b}}.\)
C.
\(\frac{{2a + b}}{{a + b}}.\)
D.
\(\frac{{a + b}}{{a + 2b}}.\)
Câu 17: 1 điểm
Tập xác định của hàm số \(y = {x^{\frac{1}{7}}}\) là
A.
\(\mathbb{R}\backslash 0.\)
B.
\(\mathbb{R}.\)
C.
\((0; + \infty ).\)
D.
\([0; + \infty ).\)
Câu 18: 1 điểm
Tập xác định của hàm số \({\rm{y}} = {{\rm{x}}^7}\) là
A.
\(\mathbb{R}\backslash 0.\)
B.
\(\mathbb{R}.\)
C.
\((0; + \infty ).\)
D.
\([0; + \infty ).\)
Câu 19: 1 điểm
Tập xác định của hàm số \({\rm{y}} = {{\rm{x}}^{ - 7}}\) là
A.
\(\mathbb{R}\backslash 0.\)
B.
\(\mathbb{R}.\)
C.
\((0; + \infty ).\)
D.
\([0; + \infty ).\)
Câu 20: 1 điểm
Tập xác định của hàm số \({\rm{y}} = {7^{\rm{x}}}\) là
A.
\(\mathbb{R}\backslash 0.\)
B.
\(\mathbb{R}.\)
C.
\((0; + \infty ).\)
D.
\([0; + \infty ).\)
Câu 21: 1 điểm
Tập xác định của hàm số \({\rm{y}} = {\log _7}{\rm{x}}\) là
A.
\(\mathbb{R}\backslash 0.\)
B.
\(\mathbb{R}.\)
C.
\((0; + \infty ).\)
D.
\([0; + \infty ).\)
Câu 22: 1 điểm
Đạo hàm của hàm số \(y = {x^7}\) là
A.
\(7{x^6}.\)
B.
\(\frac{{{x^8}}}{8}.\)
C.
\({x^6}.\)
D.
\({x^8}.\)
Câu 23: 1 điểm
Đạo hàm của hàm số \({\rm{y}} = {7^{\rm{x}}}\) là
A.
\({7^x}\ln 7.\)
B.
\({7^{{\rm{x}} - 1}}.\)
C.
\(\frac{{{7^x}}}{{\ln 7}}.\)
D.
\(({\rm{x}} - 1) \cdot {7^{{\rm{x}} - 1}}.\)
Câu 24: 1 điểm
Đạo hàm của hàm số \({\log _7}x\) là
A.
\(\frac{1}{{\rm{x}}}.\)
B.
\(\frac{1}{{{\rm{x}}\log 7}}.\)
C.
\(\frac{{\ln 7}}{x}.\)
D.
\(\frac{1}{{x\ln 7}}.\)
Câu 25: 1 điểm
Đạo hàm của hàm số \({\log _7}(1 - x)\) là
A.
\(\frac{1}{{x - 1}}.\)
B.
\(\frac{1}{{(x - 1)\log 7}}.\)
C.
\(\frac{1}{{(x - 1)\ln 7}}.\)
D.
\(\frac{1}{{(1 - x)\ln 7}}.\)
Câu 26: 1 điểm
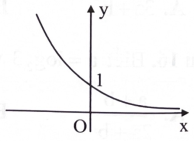
Hình bên là đồ thị hàm số nào?
A.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
B.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
C.
\(y = {\log _a}x,a > 1.\)
D.
\({\rm{y}} = {\log _{\rm{a}}}{\rm{x}},0 < {\rm{a}} < 1.\)
Câu 27: 1 điểm
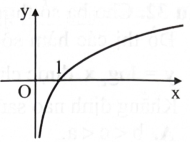
Hình bên là đồ thị hàm số nào?
A.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
B.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
C.
\(y = {\log _a}x,a > 1.\)
D.
\({\rm{y}} = {\log _a}{\rm{x}},0 < {\rm{a}} < 1.\)
Câu 28: 1 điểm
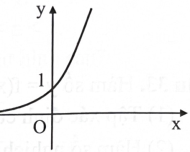
Hình bên là đồ thị hàm số nào?
A.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
B.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
C.
\(y = {\log _a}x,a > 1.\)
D.
\({\rm{y}} = {\log _a}{\rm{x}},0 < {\rm{a}} < 1.\)
Câu 29: 1 điểm
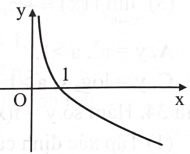
Hình bên là đồ thị hàm số nào?
A.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
B.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
C.
\(y = {\log _a}x,a > 1.\)
D.
\({\rm{y}} = {\log _a}{\rm{x}},0 < {\rm{a}} < 1.\)
Câu 30: 1 điểm
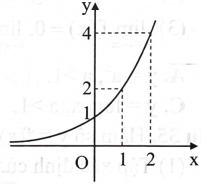
Trong các hàm số sau đây, hàm số nào có đồ thị phù hợp với hình bên?
A.
\({\rm{y}} = {{\rm{e}}^{\rm{x}}}.\)
B.
\({\rm{y}} = {2^{\rm{x}}}.\)
C.
\({\rm{y}} = {2^{ - {\rm{x}}}}.\)
D.
\(y = {e^{ - x}}.\)
Câu 31: 1 điểm
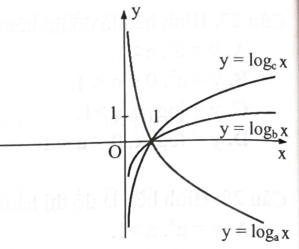
Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số \({\rm{y}} = {\log _{\rm{a}}}{\rm{x}},{\rm{y}} = {\log _{\rm{b}}}{\rm{x}}\), \({\rm{y}} = {\log _{\rm{c}}}{\rm{x}}\) được cho như hình vẽ bên. Khẳng định nào sau đây là đúng?
A.
\({\rm{b}} < {\rm{c}} < {\rm{a}}.\)
B.
\({\rm{c}} < {\rm{a}} < {\rm{b}}.\)
C.
\({\rm{a}} < {\rm{c}} < {\rm{b}}.\)
D.
\({\rm{a}} < {\rm{b}} < {\rm{c}}.\)
Câu 32: 1 điểm
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) nào sau đây có ba tính chất sau?
(1) Tập xác định của hàm số là \((0; + \infty ).\)
(2) Hàm số nghịch biến trên \(\mathbb{R}.\)
(3) \(\mathop {\lim }\limits_{x \to {0^ + }} f(x) = + \infty ,\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty .\)
A.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
B.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
C.
\(y = {\log _a}x,a > 1.\)
D.
\(y = {\log _a}x,0 < a < 1.\)
Câu 33: 1 điểm
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) nào sau đây có ba tính chất sau?
(1) Tập xác định của hàm số là \(\mathbb{R}.\)
(2) Hàm số đồng biến trên \(\mathbb{R}.\)
(3) \(\mathop {\lim }\limits_{x \to - \infty } f(x) = 0,\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty .\)
A.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
B.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
C.
\(y = {\log _a}x,a > 1.\)
D.
\(y = {\log _a}x,0 < a < 1.\)
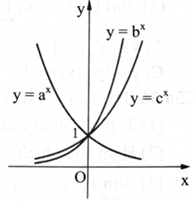
Câu 34: 1 điểm
Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số \({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{y}} = {{\rm{b}}^{\rm{x}}},{\rm{y}} = {{\rm{c}}^{\rm{x}}}\) được cho như hình vẽ bên. Khẳng định nào sau đây là đúng?
A.
\({\rm{b}} < {\rm{c}} < {\rm{a}}.\)
B.
\({\rm{a}} < {\rm{c}} < {\rm{b}}.\)
C.
\({\rm{c}} < {\rm{a}} < {\rm{b}}.\)
D.
\({\rm{a}} < {\rm{b}} < {\rm{c}}.\)
Câu 35: 1 điểm
Hàm số \(y = f(x)\) nào sau đây có ba tính chất sau?
(1) Tập xác định của hàm số là \((0; + \infty ).\)
(2) Hàm số đồng biến trên \(\mathbb{R}.\)
(3) \(\mathop {\lim }\limits_{x \to {0^ + }} f(x) = - \infty ,\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty .\)
A.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
B.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
C.
\(y = {\log _a}x,a > 1.\)
D.
\(y = {\log _a}x,0 < a < 1.\)
Câu 36: 1 điểm
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) nào sau đây có ba tính chất sau?
(1) Tập xác định của hàm số là \(\mathbb{R}.\)
(2) Hàm số nghịch biến trên \(\mathbb{R}.\)
(3) \(\mathop {\lim }\limits_{x \to - \infty } f(x) = + \infty ,\mathop {\lim }\limits_{x \to + \infty } f(x) = 0.\)
A.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
B.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
C.
\(y = {\log _a}x,a > 1.\)
D.
\(y = {\log _a}x,0 < a < 1.\)
Câu 37: 1 điểm
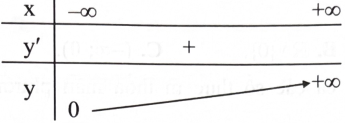
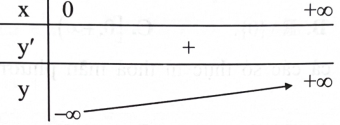
Hàm số \({\rm{y}} = {\rm{f}}({\rm{x}})\) nào sau đây có bảng biến thiên như hình sau?
A.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
B.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
C.
\(y = {\log _a}x,a > 1.\)
D.
\(y = {\log _a}x,0 < a < 1.\)
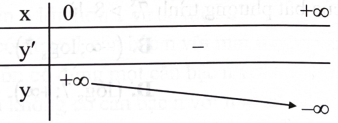
Câu 38: 1 điểm
Hàm số y=f(x) nào sau đây có bảng biến thiên như hình sau?
A.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
B.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
C.
\(y = {\log _a}x,a > 1.\)
D.
\(y = {\log _a}x,0 < a < 1.\)
Câu 39: 1 điểm
Hàm số y=f(x) nào sau đây có bảng biến thiên như hình sau?
A.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
B.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
C.
\(y = {\log _a}x,a > 1.\)
D.
\(y = {\log _a}x,0 < a < 1.\)
Câu 40: 1 điểm
Hàm số y=f(x) nào sau đây có bảng biến thiên như hình sau?
A.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},{\rm{a}} > 1.\)
B.
\({\rm{y}} = {{\rm{a}}^{\rm{x}}},0 < {\rm{a}} < 1.\)
C.
\(y = {\log _a}x,a > 1.\)
D.
\(y = {\log _a}x,0 < a < 1.\)
Tuyển tập bộ đề
Đề thi tương tự
Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Hóa Bài 9. Vật liệu polymer có đáp án
1 mã đề 20 câu hỏi
Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Hóa Bài 11. Nguồn điện hóa học có đáp án
1 mã đề 59 câu hỏi
Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Hóa Bài 2. Xà phòng và chất giặt rửa tổng hợp có đáp án
1 mã đề 27 câu hỏi
Trắc nghiệm tổng hợp ôn thi tốt nghiệp THPT môn Toán Chủ đề 3: Vectơ, phương pháp toạ độ trong không gian có đáp án
6 mã đề 147 câu hỏi