Trang chủ Đề thi Lớp 11 Toán học 11612

Ôn Tập Toán 11 Chương 5: Đạo Hàm 100 Câu Trắc Nghiệm Cơ Bản

Bộ 100 câu trắc nghiệm ôn tập môn Toán lớp 11, chương 5 về đạo hàm cơ bản. Bao gồm các bài tập về định nghĩa đạo hàm, quy tắc tính đạo hàm, đạo hàm của hàm số cơ bản và ứng dụng đạo hàm trong khảo sát hàm số. Tài liệu phù hợp để học sinh luyện tập, củng cố kiến thức và chuẩn bị cho các kỳ kiểm tra, thi học kỳ. Có đáp án chi tiết hỗ trợ tự học hiệu quả.

Từ khoá: toán 11 đạo hàm trắc nghiệm đạo hàm ôn tập toán 11 bài tập đạo hàm khảo sát hàm số học toán lớp 11 đề thi toán 11 toán phổ thông ôn thi học kỳ

Số câu hỏi: 124 câuSố mã đề: 5 đềThời gian: 1 giờ

151,344 lượt xem 11,616 lượt làm bài

Xem trước nội dung
Câu 1: 1 điểm

Cho hàm số 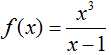Hình ảnh. Tập nghiệm của phương trình f’(x) = 0 là

A.  
B.  
C.  
D.  
Câu 2: 1 điểm

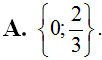
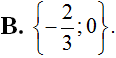
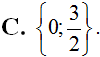
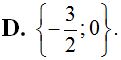
Tìm số f(x) = x3 – 3x2 + 1. Đạo hàm của hàm số f(x) âm khi và chỉ khi.

A.  
0 < x < 2.
B.  
x < 1.
C.  
x < 0 hoặc x > 1
D.  
x < 0 hoặc x > 2.
Câu 3: 1 điểm

Cho hàm số Hình ảnh. Để y’ > 0 thì x nhận các giá trị thuộc tập nào sau đây?

A.  
(-∞; +∞).
B.  
C.  
D.  
∅.
Câu 4: 1 điểm

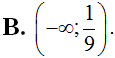
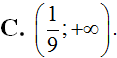
Cho hàm số y = (2x2 + 1)3. Để y’ ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây?

A.  
∅.
B.  
(-∞; 0].
C.  
[0; +∞).
D.  
R
Câu 5: 1 điểm

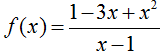Cho hàm số Hình ảnh. Để y’ ≤ 0 thì x nhận các giá trị thuộc tập nào sau đây?

A.  
∅.
B.  
(-∞; 0).
C.  
 (0; +∞).
D.  
(-∞; 0].
Câu 6: 1 điểm

Cho hàm số Hình ảnh . Tập nghiệm của bất phương trình f’(x) > 0 là

A.  
R \ {1}.
B.  
∅.
C.  
(1; +∞).
D.  
 R.
Câu 7: 1 điểm

Cho hàm số y = x3. Viết tiếp tuyến của đồ thị hàm số đã cho. Biết tiếp điểm là M(1; 1).

A.  
A: y = 3x + 1
B.  
B: y = 3x - 1
C.  
C: y = 3x + 2
D.  
D: y = 3x - 2
Câu 8: 1 điểm

Cho hàm số y = x3. Viết tiếp tuyến của đồ thị hàm số đã cho. Biết hoành độ tiếp điểm bằng 2.

A.  
A: y = 12x + 1
B.  
B: y = 12x - 16
C.  
C: y = 6x + 2
D.  
D: y = 6x - 12
Câu 9: 1 điểm

Cho hàm số 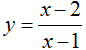Hình ảnh  . Viết PTTT của đồ thị hàm số biết . Tiếp điểm M có tung độ bằng 4

A.  
A: y = 9x + 2
B.  
B: y = 9x - 16
C.  
C: y = 9x + 8
D.  
D: y = 9x - 2
Câu 10: 1 điểm

Cho hàm số 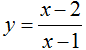Hình ảnh . Viết PTTT của đồ thị hàm số biết. Tiếp điểm M là giao điểm của đồ thị hàm số với trục tung

A.  
A: y = 2x + 1
B.  
B: y = 2x - 6
C.  
C: y = x + 2
D.  
D: y = x - 12
Câu 11: 1 điểm

Cho hàm số y = x3 + x2 + x + 1. Viết PTT tại Mthuộc đồ thị hàm số biết tung độ điểm M bằng 1.

A.  
A: y = 2x + 1
B.  
B: y = x + 1
C.  
C: y = x + 2
D.  
D: y = x - 1
Câu 12: 1 điểm

Cho hàm số 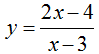Hình ảnh  có đồ thị là (H). Phương trình tiếp tuyến tại giao điểm của (H)  với trục hoành là:

A.  
y = 2x – 4.
B.  
y = 3x + 1.
C.  
y = - 2x + 4.
D.  
y = 2x.
Câu 13: 1 điểm

Phương trình tiếp tuyến của đồ thị hàm số f(x) = x3 – 2x2 + 3x tại điểm có hoành độ xo = -1 là:

A.  
y = 10x + 4.
B.  
y = 10x – 5.
C.  
y = 2x – 4.
D.  
y = 2x – 5.
Câu 14: 1 điểm

Trong các tiếp tuyến tại các điểm trên đồ thị hàm số y = x3 – 3x2 + 2, tiếp tuyến có hệ số góc nhỏ nhất bằng

A.  
A. -3
B.  
B. 3
C.  
C. 4
D.  
D. 0
Câu 15: 1 điểm

Phương trình tiếp tuyến của đồ thị hàm số y = x4 + 2x2 – 1 tại điểm có tung độ tiếp điểm bằng 2 là:

A.  
y = 8x – 6, y = -8x – 6.
B.  
y = 8x = 6, y = -8x + 6.
C.  
y = 8x – 8, y = -8x + 8.
D.  
y = 40x – 57.
Câu 16: 1 điểm

Cho hàm số 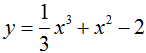Hình ảnh  có đồ thị hàm số (C). Phương trình tiếp tuyến của (C) tại điểm có hoành độ là nghiệm của phương trình y” = 0 là

A.  
B.  
C.  
D.  
Câu 17: 1 điểm

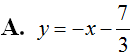
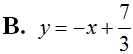
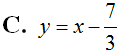
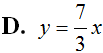
Cho hàm số 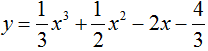Hình ảnh.Viết phương trình tiếp tuyến với đồ thị hàm số biết tiếp tuyến song song với đường thẳng d: 4x – y + 2 = 0.

A.  
y = 4x – 6, y = -4x – 4.
B.  
y = 4x – 6, y = -4x + 6.
C.  
y = 2x – 8, y = -2x + 8.
D.  
Tất cả sai
Câu 18: 1 điểm

Cho hàm số 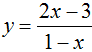Hình ảnh. Viết phương trình tiếp tuyến với đồ thị hàm số biết tiếp tuyến vuông góc với đường thẳng d : x – y + 2017 = 0

A.  
y = - x – 3, y = -x – 1.
B.  
y = -x – 3, y = -x + 1.
C.  
y = -x – 8, y = - x + 8.
D.  
Tất cả sai
Câu 19: 1 điểm

Cho hàm số y = 3 x - 2 x - 2 .Viết phương trình tiếp tuyến d với đồ thị hàm số biết d tạo với trục hoành một góc α mà 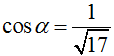Hình ảnh

A.  
y = -4x – 19, y = -4x – 1.
B.  
y = -4x + 19, y = -x + 3.
C.  
y = -4x + 19, y = -4x + 3.
D.  
Tất cả sai
Câu 20: 1 điểm

Cho hàm số y = x2 – 6x + 5 có tiếp tuyến song song với trục hoành. Phương trình tiếp tuyến đó là:

A.  
x = -3.
B.  
y = -4.
C.  
y = 4.
D.  
x = 3.
Câu 21: 1 điểm

Tiếp tuyến của đồ thị hàm số 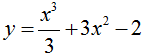Hình ảnh  có hệ số góc k = -9có phương trình là:

A.  
y – 16 = -9(x + 3).
B.  
y = -9(x + 3).
C.  
y – 16 = -9(x – 3).
D.  
y + 16 = -9(x + 3).
Câu 22: 1 điểm

Cho hàm số 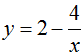Hình ảnh  có đồ thị (H). Đường thẳng Δ vuông góc với đường thẳng d: y = -x + 2 và tiếp xúc với (H) thì phương trình của Δlà

A.  
y = x + 4.
B.  
C.  
D.  
Không tồn tại.
Câu 23: 1 điểm

Lập phương trình tiếp tuyến của đường cong (C):  y = x3 + 3x2 – 8x + 1, biết tiếp tuyến đó song song với đường thẳng Δ: y = x + 2017?

A.  
y = x + 2018.
B.  
y = x + 4.
C.  
y = x – 4; y = x + 28.
D.  
y = x - 2018.
Câu 24: 1 điểm

Cho hàm số y = -x3 + 3x2 – 2 có đồ thị (C). Số tiếp tuyến của (C) song song với đường thẳng y = -9x  là:

A.  
1.
B.  
3.
C.  
4.
D.  
2.
Câu 25: 1 điểm

Cho hàm số y = x3 – 2x2 + 2x có đồ thị (C). Gọi x1, x2 là hoành độ các điểm M, N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2017. Khi đó x1 + x2 bằng:

A.  
4/3.
B.  
-4/3.
C.  
1/3.
D.  
-1.