Trang chủ Đề thi Toán học 14319

Trắc nghiệm Ôn tập chương 3 có đáp án

Trắc nghiệm tổng hợp Toán 11
Tổng hợp trắc nghiệm Toán 11 có lời giải
Lớp 11;Toán

Số câu hỏi: 13 câuSố mã đề: 1 đềThời gian: 1 giờ

186,255 lượt xem 14,319 lượt làm bài

Xem trước nội dung
Câu 1: 1 điểm

Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.

Bộ ba vecto đồng phẳng là:

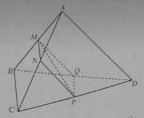
Hình ảnh

A.  
A B → ,   B C → ,   A D →
B.  
M P → ,   B C → ,   A D →
C.  
A C → ,   M P → ,   B D →
D.  
M P → ,   P Q → ,   C D →
Câu 2: 1 điểm

Cho tứ diện ABCD. Gọi M, N, P, và Q lần lượt là trung điểm của AB, AC, CD và DB.

Bộ ba vecto không đồng phẳng là:

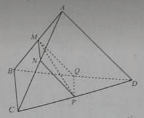
Hình ảnh

A.  

A.  A B → ,   M N → ,   C A →

B.  
  M P → ,   B C → ,   A D →
C.  
  A D → ,   M P → ,   P Q →
D.  
  M P → ,   P Q → ,   P D →
Câu 3: 1 điểm

Điều kiện cần và đủ để ba vecto a → ,   b → ,   c → không đồng phẳng là:

A.  
Ba đường thẳng chứa chúng không cùng thuộc một mặt phẳng.
B.  
Ba đường thẳng chứa chúng cùng thuộc một mặt phẳng.
C.  
Ba đường thẳng chứa chúng không cùng song song với một mặt phẳng.
D.  
Ba đường thẳng chứa chúng cùng song song với một mặt phẳng.
Câu 4: 1 điểm

Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Không thể kết luận được điểm G là trọng tâm của tứ diện ABCD trong trường hợp

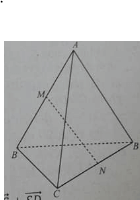
Hình ảnh

A.  
GM = GN
B.  
  G M →   +   G N →   =   0 →
C.  

C.  G A →   +   G B →   +   G C →   +   G D →   =   0

D.  
P G →   =   1 / 4 ( P A →   +   P B →   +   P C →   +   P D → ) , với P là điểm bất kì.
Câu 5: 1 điểm

Cho hình chóp S.ABCD, với O là giao điểm của AC và BD. Mệnh đề nào sau đây là đúng?

A.  

A. Nếu ABCD là hình bình hành thì  S A →   +   S B →   =   S C →   +   S D →

B.  
Nếu SA + SC = SB + SD thì ABCD là hình bình hành.
C.  
C. Nếu ABCD là hình bình hành thì  S A →   +   S B →   +   S C →   +   S D →   =   0
D.  
D. Nếu  S A →   +   S B →   +   S C →   +   S D →   =   4 S O →
Câu 6: 1 điểm

Các đường thẳng cùng vuông góc với một đương thẳng thì:

A.  
Thuộc một mặt phẳng
B.  
Vuông góc với nhau
C.  
Song song với một mặt phẳng
D.  
Song song với nhau
Câu 7: 1 điểm

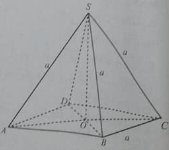
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.

Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD) vì:

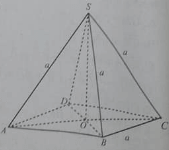
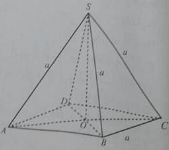
Hình ảnh

A.  
AC ⊂ (SAC) và AC ⊥ (SBD) do AC ⊥ SO và AC ⊥ BD
B.  
AC ⊂ (ABCD) và AC ⊥ (SBD) do AC ⊥ SO và AC ⊥ BD
C.  
AC ⊂ (SAC) và AC ⊥ SO ⊂ (SBD)
D.  
D. AC ⊂ (ABCD) và AC ⊥ SO ⊂ (SBD) và góc AOS bằng  90 o
Câu 8: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.

Giả sử góc BAD bằng 60 o , khoảng cách từ S đến mặt phẳng (ABCD) bằng:

Hình ảnh

A.  
a 2
B.  
a 3 2
C.  
a
D.  
a 3
Câu 9: 1 điểm

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.

Góc giữa hai mặt bên hình chóp S.ABCD và mặt phẳng đáy có tan bằng:

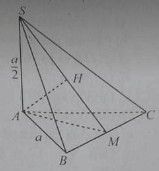
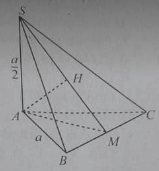
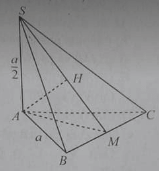
Hình ảnh

A.  
1
B.  
3
C.  
3 2
D.  
2 3 3
Câu 10: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.

Góc giữa hai mặt phẳng (SAB) và (ABC) bằng:

Hình ảnh

A.  

A. 0 o

B.  
45 o
C.  
60 o
D.  
90 o
Câu 11: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.

M là trung điểm của BC. Khi đó góc giữa hai mặt phẳng (SAM) và (SBC) bằng:

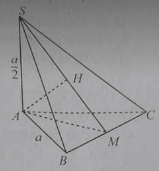
Hình ảnh

A.  

A.  0 o

B.  
30 o
C.  
45 o
D.  
60 o
Câu 12: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.

Từ A hạ AH ⊥ SM. Khi đó góc giữa hai vecto  S A →  và  A H →  bằng:

Hình ảnh

A.  

A.  40 o

B.  
45 o
C.  
90 o
D.  
150 o
Câu 13: 1 điểm

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a/2.

Góc giữa hai mặt phẳng (SAB) và (SAC) bằng:

Hình ảnh

A.  

A. 0 o

B.  
45 o
C.  
60 o
D.  
90 o