Trang chủ Đề thi 29238

Tồng hợp đề thi chính thức môn Toán THPT năm 2025 đề 01 - 12

Khám phá và luyện tập với bộ 12 đề thi trắc nghiệm Toán tốt nghiệp THPT năm 2025 (mã đề 0101–0112). Nội dung bám sát cấu trúc đề thi chính thức, kèm đáp án chi tiết giúp bạn tự đánh giá năng lực, rèn kỹ năng giải nhanh và tự tin đạt điểm cao.

Từ khoá: thi Toán 2025 đề thi trắc nghiệm Toán tốt nghiệp THPT ôn thi tốt nghiệp THPT luyện thi Toán online đáp án chi tiết Toán THPTbộ đề toán 0101 - 0112

Số câu hỏi: 198 câuSố mã đề: 10 đềThời gian: 1 giờ 30 phút

380,120 lượt xem 29,238 lượt làm bài


Bạn chưa làm Đề 0101!

Xem trước nội dung
Câu 1: 0.45 điểm

Cho hình lăng trụ ABC A′B′C′ABC\,A'B'C' (xem hình dưới). Phát biểu nào sau đây là đúng?

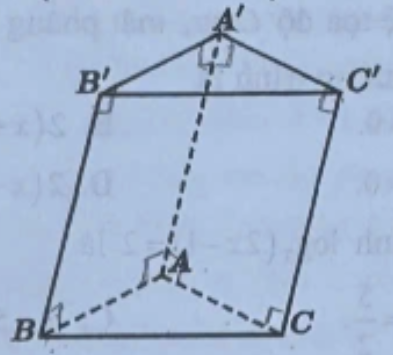
Hình ảnh
A.  
BA→+A′C′→=BC′→\overrightarrow{BA} + \overrightarrow{A'C'} = \overrightarrow{BC'}
B.  
BA→+A′C′→=C′B→\overrightarrow{BA} + \overrightarrow{A'C'} = \overrightarrow{C'B}
C.  
BA→+A′C′→=BC→\overrightarrow{BA} + \overrightarrow{A'C'} = \overrightarrow{BC}
D.  
BA→+A′C′→=A′A→\overrightarrow{BA} + \overrightarrow{A'C'} = \overrightarrow{A'A}
Câu 2: 0.45 điểm

Cho hình hộp ABCD A′B′C′D′ABCD\,A'B'C'D' (xem hình dưới). Đường thẳng AB song song với mặt phẳng nào sau đây?

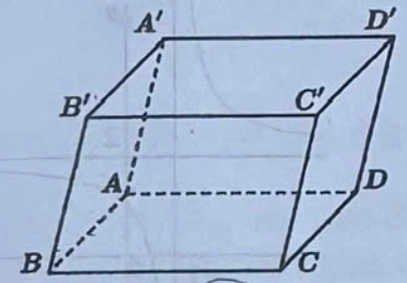
Hình ảnh
A.  
(CC′A′A)(CC'A'A)
B.  
(BB′C′C)(BB'C'C)
C.  
(A′B′C′D′)(A'B'C'D')
D.  
(AA′D′D)(AA'D'D)
Câu 3: 0.45 điểm

Một người chia thời lượng (đơn vị: giây) thực hiện các cuộc gọi điện thoại của mình trong một tuần thành sáu nhóm và lập bảng tần số ghép nhóm như sau: 

Hình ảnh

Tứ phân vị thứ ba Q3Q_3 (đơn vị: giây) của mẫu số liệu ghép nhóm trên bằng

A.  
145
B.  
140
C.  
135
D.  
130
Câu 4: 0.45 điểm
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng (d): x+34=y+2−5=z+12\frac{x+3}{4} = \frac{y+2}{-5} = \frac{z+1}{2}. Vector nào sau đây là một vector chỉ phương của đường thẳng (d)?
A.  
v3=(4;5;2)v_3 = (4;5;2)
B.  
v1=(3;−2;1)v_1 = (3;-2;1)
C.  
v4=(3;2;1)v_4 = (3;2;1)
D.  
v2=(4;−5;2)v_2 = (4;-5;2)
Câu 5: 0.45 điểm
Họ nguyên hàm của hàm số f(x)=x2f(x) = x^2 là
A.  
13x3+C\frac{1}{3}x^3 + C
B.  
2x3+C2x^3 + C
C.  
3x3+C3x^3 + C
D.  
12x3+C\frac{1}{2}x^3 + C
Câu 6: 0.45 điểm
Cho cấp số cộng (un)(u_n) có u1=4u_1 = 4 và công sai d=−3d = -3. Giá trị của u5u_5 bằng
A.  
16
B.  
19
C.  
-8
D.  
-11
Câu 7: 0.45 điểm
Tập nghiệm của phương trình sin⁡x=0\sin x = 0 là
A.  
S={π2+kπ∣k∈Z}S = \{\tfrac{\pi}{2} + k\pi \mid k\in\mathbb{Z}\}
B.  
S={k2π∣k∈Z}S = \{k2\pi \mid k\in\mathbb{Z}\}
C.  
S={−π2+k2π∣k∈Z}S = \{-\tfrac{\pi}{2} + k2\pi \mid k\in\mathbb{Z}\}
D.  
S={kπ∣k∈Z}S = \{k\pi \mid k\in\mathbb{Z}\}
Câu 8: 0.45 điểm
Trong mặt phẳng với hệ tọa độ Oxy, diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y=2x−3y = 2x - 3, trục hoành và hai đường thẳng x=1x = 1, x=2x = 2 được xác định bằng công thức
A.  
S=π∫12∣2x−3∣ dxS = \pi\int_{1}^{2}\lvert 2x - 3\rvert\,dx
B.  
S=∫12∣2x−3∣ dxS = \int_{1}^{2}\lvert 2x - 3\rvert\,dx
C.  
S=π∫12(2x−3)2 dxS = \pi\int_{1}^{2}(2x - 3)^2\,dx
D.  
S=∫12(2x−3) dxS = \int_{1}^{2}(2x - 3)\,dx
Câu 9: 0.45 điểm
Trong không gian với hệ tọa độ Oxyz, mặt phẳng đi qua điểm A(2;1;−4)A(2;1;-4) nhận vectơ pháp tuyến n=(3;2;−1)n = (3;2;-1) có phương trình là
A.  
3(x−2)+2(y−1)−(z+4)=03(x - 2) + 2(y - 1) - (z + 4) = 0
B.  
2(x+3)+(y+2)−4(z−1)=02(x + 3) + (y + 2) - 4(z - 1) = 0
C.  
3(x+2)+2(y+1)−(z−4)=03(x + 2) + 2(y + 1) - (z - 4) = 0
D.  
2(x−3)+(y−2)−4(z+1)=02(x - 3) + (y - 2) - 4(z + 1) = 0
Câu 10: 0.45 điểm
Nghiệm của phương trình log⁡3(2x−1)=2\log_{3}(2x - 1) = 2 là
A.  
x=72x = \tfrac{7}{2}
B.  
x=52x = \tfrac{5}{2}
C.  
x=5x = 5
D.  
x=4x = 4
Câu 11: 0.45 điểm

Cho hàm số y=ax+bcx+dy = \frac{ax + b}{cx + d} (ac ≠ 0, ad - bc ≠ 0) có đồ thị như hình dưới. Đường tiệm cận đứng của đồ thị hàm số đã cho có phương trình là
 

Hình ảnh
A.  
y=2y = 2
B.  
x=−1x = -1
C.  
y=−1y = -1
D.  
x=2x = 2
Câu 12: 0.45 điểm
Cho hình chóp S.ABCS.ABC có SA⊥(ABC)SA \perp (ABC), tam giác ABCABC vuông tại AA và SA=3, AB=4, AC=5SA = 3,\, AB = 4,\, AC = 5. Thể tích của khối chóp S.ABCS.ABC bằng
A.  
30
B.  
20
C.  
60
D.  
10
Câu 13: 0.45 điểmchọn đúng/sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hàm số f(x)=x3−12x−8f(x) = x^3 - 12x - 8.

A.
 
a. Hàm số đã cho có đạo hàm là f′(x)=3x2−12f'(x) = 3x^2 - 12.
B.
 
b. Phương trình f′(x)=0f'(x) = 0 có tập nghiệm là S={2}S = \{2\}.
C.
 
c. f(2)=24f(2) = 24.
D.
 
d. Giá trị lớn nhất của hàm số f(x)f(x) trên đoạn [−3;3][-3;3] bằng 24.
Câu 14: 0.45 điểmchọn đúng/sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Đối với ngành nuôi trồng thủy sản, người ta theo dõi nồng độ thuốc tồn dư y(t)y(t) (mg/lít) tại thời điểm tt (ngày, t≥0t\ge0) sau một lần sử dụng thuốc. Kết quả thỏa mãn y′(t)=k y(t)y'(t) = k\,y(t) với keq0k eq0, và biết y(t)=eg(t)y(t) = e^{g(t)}. Khi t=6t=6, y(6)=2y(6)=2; khi t=12t=12, y(12)=1y(12)=1.

A.
 
a. g′(t)=k+Cg'(t) = k + C (với CC là hằng số xác định).
B.
 
b. k=ln⁡26k = \frac{\ln 2}{6}.
C.
 
c. C=2ln⁡2C = 2\ln 2.
D.
 
d. Nồng độ thuốc tồn dư tại t=25t = 25 (ngày) lớn hơn 0,25 mg/lít.
Câu 15: 0.45 điểmchọn đúng/sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Mô hình toán học quan sát chuyển động của một vật trong không gian OxyzOxyz: cho điểm A(5;5;0)A(5;5;0), vectơ đơn vị i,j,ki,j,k có độ dài 1 m, vận tốc v(t)=βt+300v(t)=\beta t+300 (m/s) với 0≤t≤60\le t\le6. Vật đi qua A khi t=0t=0 với vận tốc 300 m/s hướng về B. Sau 2 giây, vật đi được 604 m. Gọi u=(a;b;c)u=(a;b;c) là vectơ đơn vị cùng hướng AB→\overrightarrow{AB}, biết ∣u∣=1|u|=1 và góc giữa uu với các vectơ i,j,ki,j,k lần lượt là 60°, 60°, 45°.

A.
 
a. a=cos⁡60∘a = \cos60^\circ.
B.
 
b. Phương trình đường thẳng AB là x−51=y−51=z2\frac{x-5}{1} = \frac{y-5}{1} = \frac{z}{2}.
C.
 
c. β=2\beta = 2.
D.
 
d. Sau 5 giây, nếu điểm B có tọa độ (xB;yB;zB)(x_B;y_B;z_B) thì xB>768x_B > 768.
Câu 16: 0.45 điểmchọn đúng/sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Một phần mềm nhận dạng tin nhắn quảng cáo: 15% tin nhắn được đánh dấu. Trong số đã đánh dấu, 10% không phải quảng cáo. Trong số không đánh dấu, 5% là quảng cáo. Chọn ngẫu nhiên một tin nhắn đến.

A.
 
a. Xác suất tin nhắn đó không bị đánh dấu bằng 0,85.
B.
 
b. Xác suất tin nhắn đó không phải quảng cáo, biết rằng nó không bị đánh dấu, bằng 0,95.
C.
 
c. Xác suất tin nhắn đó không bị đánh dấu và là quảng cáo bằng 0,85.
D.
 
d. Xác suất tin nhắn đó không bị đánh dấu, biết rằng nó không phải quảng cáo, lớn hơn 0,95.
Câu 17: 0.45 điểm

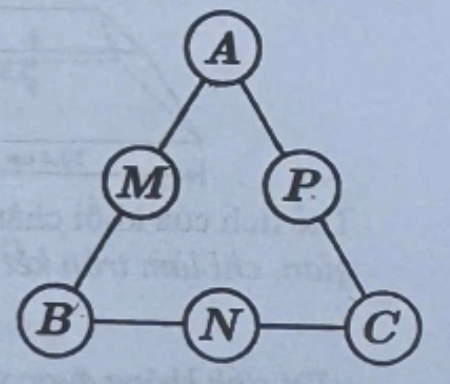
Bạn Nam tham gia cuộc thi giải một mật thư. Theo quy tắc của cuộc thi, người chơi cần chọn ra sáu số từ tập S={11,12,13,14,15,16,17,18,19}S=\{11,12,13,14,15,16,17,18,19\} và xếp mỗi số vào đúng một vị trí trong sáu vị trí A, B, C, M, N, P như hình bên sao cho mỗi vị trí chỉ được xếp một số. Mật thư sẽ được giải nếu các bộ ba số xuất hiện ở các vị trí (A,M,B), (B,N,C), (C,P,A) tạo thành các cấp số cộng theo thứ tự đó. Bạn Nam chọn ngẫu nhiên sáu số trong tập S và xếp ngẫu nhiên vào các vị trí yêu cầu. Gọi xác suất để bạn Nam giải được mật thư ở lần chọn đó là aa. Giá trị của 1a\frac{1}{a} bằng bao nhiêu?

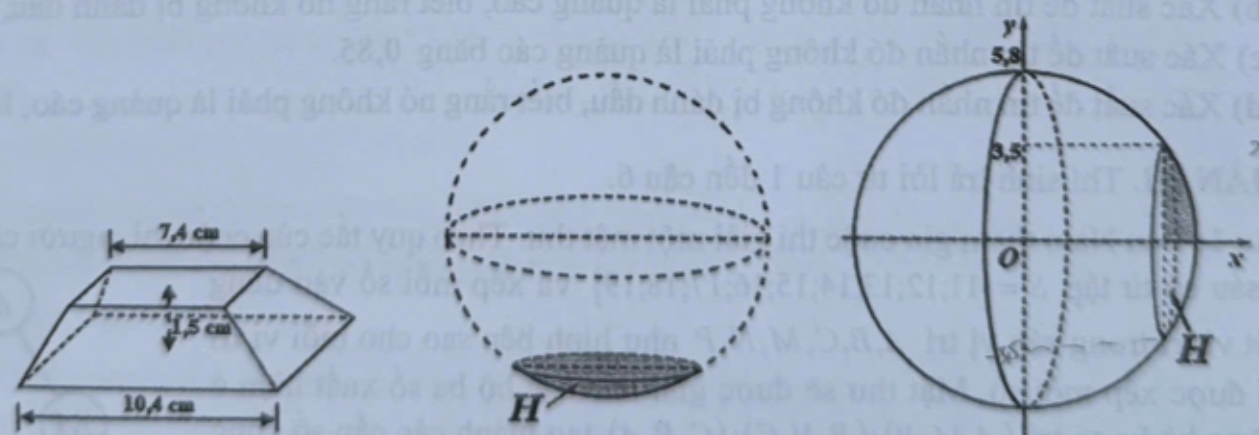
Hình ảnh
Câu 18: 0.45 điểm
Nếu một doanh nghiệp sản xuất xx sản phẩm trong một tháng (x∈N∗, 1≤x≤4500x\in\mathbb{N}^*,\,1\le x\le4500) thì doanh thu (nghìn đồng) khi bán hết số sản phẩm đó là F(x)=−0,01x2+300xF(x)=-0,01x^2+300x, trong khi chi phí sản xuất bình quân cho mỗi sản phẩm là G(x)=30000x+200G(x)=\frac{30000}{x}+200 (nghìn đồng). Giả sử số sản phẩm sản xuất ra luôn được bán hết. Trong một tháng, doanh nghiệp cần sản xuất ít nhất bao nhiêu sản phẩm để lợi nhuận thu được lớn hơn 100 triệu đồng?
Câu 19: 0.45 điểm
Để gây quỹ từ thiện, câu lạc bộ thiện nguyện của một trường THPT tổ chức bán hàng với hai thực đơn: - Thực đơn 1 giá 30 nghìn đồng, gồm hai cốc nước chanh và một túi khoai chiên. - Thực đơn 2 giá 50 nghìn đồng, gồm ba cốc nước chanh và hai túi khoai chiên. Biết câu lạc bộ chỉ làm được không quá 165 cốc nước chanh và 100 túi khoai chiên. Số tiền lớn nhất (nghìn đồng) mà câu lạc bộ có thể thu được sau khi bán hết là bao nhiêu?
Câu 20: 0.45 điểm
Cho hình chóp S.ABCDS.ABCD có đáy ABCDABCD là hình thoi với ∠ABC=60∘\angle ABC=60^\circ và AB=2AB=2. Biết hình chiếu vuông góc của S lên mặt phẳng (ABCD)(ABCD) là trọng tâm HH của tam giác ABCABC và SH=3SH=\sqrt{3}. Khoảng cách giữa hai đường thẳng ACAC và SDSD bằng bao nhiêu? (Chỉ làm tròn kết quả cuối cùng đến hàng phần trăm.)
Câu 21: 0.45 điểm
Có bốn ngăn số thứ tự 1,2,3,4 và bảy quyển sách khác nhau. Bạn An xếp hết bảy quyển vào bốn ngăn sao cho mỗi ngăn có ít nhất một quyển và các sách được xếp thẳng đứng thành một hàng ngang (gáy sách quay ra ngoài). Hai cách xếp được gọi là giống nhau nếu với từng ngăn, số lượng sách và thứ tự từ trái sang phải đều giống nhau. Gọi T là số cách xếp khác nhau (theo định nghĩa trên). Giá trị của T100\tfrac{T}{100} bằng bao nhiêu?
Câu 22: 0.45 điểm

Để làm chân đế trang trí, người ta dùng khối gỗ là hình chóp cụt tứ giác đều, hai đáy là hình vuông cạnh 7,4 cm7,4\text{ cm} và 10,4 cm10,4\text{ cm}, chiều cao 1,5 cm1,5\text{ cm}. Sau đó khoét bỏ một phần có dạng vật thể H, trong đó H là phần khối cầu bán kính 5,8 cm5,8\text{ cm} bị cắt bởi mặt phẳng sao cho mặt cắt là hình tròn bán kính 3,5 cm3,5\text{ cm}. Thể tích của khối chân đế còn lại bằng bao nhiêu (cm3), làm tròn kết quả cuối cùng đến hàng phần mười?

Hình ảnh