Bài tập Số phức cực hay có lời giải chi tiết

Cho i là đơn vị ảo. Với $x,y\in \mathrm{ℝ}$ thì x - 1 + (y + 3)i  là số thuần ảo khi và chỉ khi

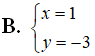
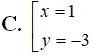
Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn |z - i + 1| = |z + i - 2| là đường thẳng có phương trình

Cho i là đơn vị ảo. Cho $m\in \mathrm{ℝ}$. Trên mặt phẳng tọa độ Oxy, điểm biểu diễn hình học số phức z = mi có tọa độ là

Cho i là đơn vị ảo. Giá trị của biểu thức $z = {\left(i^5+i^4+i^3+i^2+i+1\right)}^{40}$ là

Gọi z₁, z₂ là các nghiệm của phương trình  $z^2 -2z + 6 = 0$. Tính  $P = {z_1}^{4 } + {z_2}^4$

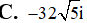
Cho số phức $z= \frac{1-i}{1+i}$. Phần thực của số phức  $z^{2017}$ là

Trong mặt phẳng tọa độ Oxy, tập hợp các điểm M biểu diễn số phức z thỏa mãn điều kiện $\left.z +1\right| \le 2$ là

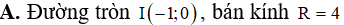
Cho số phức z thỏa mãn điều kiện $\left(z +1\right)\left(i-\overline{z}\right)$ là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng

Gọi S là tập hợp những điểm biểu diễn số phức z thỏa mãn $\left.z-1-i\right|=1$. Cho P là một điểm chạy trên S. Khi đó số phức tương ứng với P có môđun lớn nhất bằng ?

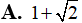
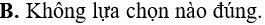
Phần thực của số phức  $w= 1+ \left(1+i\right)+{\left(1+i\right)}^2+{\left(1+i\right)}^3+...+{\left(1+i\right)}^{1999}$ bằng

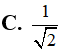
Cho ba điểm A, B, M lần lượt là các điểm biểu diễn của các số phức -2, 4i,  x+2i. Với giá trị nào của x thì A, B, M thẳng hàng.

Số phức z thỏa mãn $(2 + 3i)\overline{z} + \left(1-i\right)z = 3+5i$ Tìm môđun của số phức z.

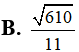
Cho z = 1 + 2i, số phức $z^{,}$ đối xứng với số phức z qua gốc tọa độ O (0;0) là

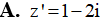
Cho số phức z = a+bi ; a,b $\in \mathrm{ℝ}$. Nhận xét nào sau đây luôn đúng?

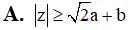
Trên mặt phẳng tọa độ Oxy, tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện $\left.zi-\left(1-2i\right)\right|=4$ là

Số phức liên hợp của số phức $z = \left(1+i\right)\left(4-3i\right)$ là