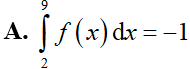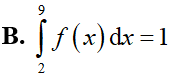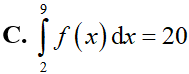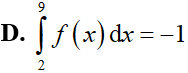186 Bài trắc nghiệm Nguyên hàm, tích phân cực hay có lời giải

Cho hai số thực a, b tùy ý, F(x) là một nguyên hàm của hàm số f(x) trên tập $\mathrm{ℝ}$. Mệnh đề nào dưới đây là đúng?

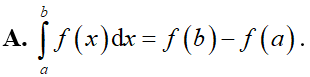
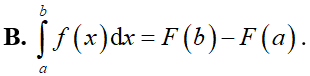
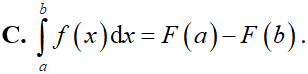
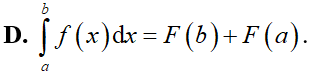
Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Mệnh đề nào dưới đây sai?

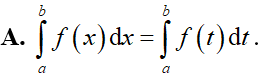
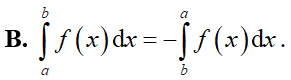
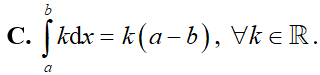
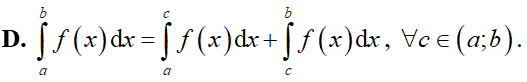
Cho hàm số f(x) liên tục trên $\mathrm{ℝ}$ và có một nguyên hàm là F(x). Biết F(2) = –7. Giá trị của F(4) là:

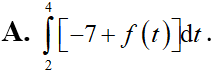
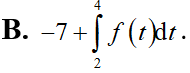
Cho hàm số y = f(x), y = g(x) là các hàm số có đạo hàm và liên tục trên[0; 2] và  ${\int }_0^{2}g\left(x\right)f^{\text{'}}\left(x\right)dx=2, {\int }_0^2{g}^{\text{'}}\left(x\right)f\left(x\right)dx=3$. Tính tích phân  $I = {\int }_0^2{\left[g\left(x\right)f\left(x\right)\right]}^{\text{'}}dx$.

Tính tích phân  ${\int }_1^2\left(2ax+b\right)dx$.

Cho f, g là hai hàm liên tục trên[1; 3] thỏa điều kiện  ${\int }_1^3\left.f\left(x\right)+3g\left(x\right)\right]dx=10$ đồng thời  ${\int }_1^3\left.2f\left(x\right)-g\left(x\right)\right]dx=6$. Tính  ${\int }_1^3\left.f\left(x\right)+g\left(x\right)\right]dx$.

Cho biết  ${\int }_a^{b}f\left(x\right)dx=2, {\int }_a^{b}g\left(x\right)dx=-3$. Giá trị của  $M={\int }_a^b\left.5f\left(x\right)+3g\left(x\right)\right]dx$ bằng

Cho  ${\int }_1^2\left.3f\left(x\right)+2g\left(x\right)\right]dx=1,{\int }_1^2\left.2f\left(x\right)-g\left(x\right)\right]dx=-3$. Khi đó,  ${\int }_1^{2}f\left(x\right)dx$ bằng

Cho hàm số f(x) có đạo hàm trên $\mathrm{ℝ}$ thỏa mãn f’(x) – 2018f(x) = 2018.x²⁰¹⁷.e^2018x  với mọi $x\in \mathrm{ℝ}$ và f(0) = 2018. Tính giá trị f(1).

Cho hàm số f(x) liên tục trên $\mathrm{ℝ}$ và F(x) là nguyên hàm của f(x), biết ${\int }_0^{9}f\left(x\right)dx=9$và F(0) = 3. Giá trị của F(9) bằng

Nếu  ${\int }_2^{5}f\left(x\right)dx=3, {\int }_5^{7}f\left(x\right)dx=9$ thì  ${\int }_2^{7}f\left(x\right)dx$ bằng bao nhiêu?

Tính tích phân  $I={\int }_1^2\frac{dx}{x}$

Có bao nhiêu số thực b thuộc khoảng $\left(\pi ,3\pi \right)$ sao cho  ${\int }_{\pi }^{b}4\cos 2xdx=1$

Cho hàm số f(x) có đạo hàm liên tục trên đoạn [a;b] và f(a) = –2, f(b) = –4. Tính  $T={\int }_a^b{f}^{\text{'}}\left(x\right)dx$.

Cho hàm số f(x) có đạo hàm liên tục trên đoạn [1;3] thỏa mãn f(1) = 2 và f(3) = 9. Tính  $I={\int }_1^3{f}^{\text{'}}\left(x\right)dx$.

Cho  ${\int }_a^{c}f\left(x\right)dx=17,{\int }_b^{c}f\left(x\right)dx=-11$ với a < b < c. Tính  $I={\int }_a^{b}f\left(x\right)dx$.

Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn[–1;1] thỏa mãn ${\int }_{-1}^1{f}^{\text{'}}\left(x\right)dx=5$ và f(–1) = 4. Tìm f(1).

Chọn khẳng định sai trong các khẳng định sau:

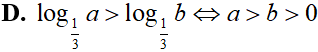
Trong các mệnh đề sau,mệnh đề nào sai?

Cho a, b > 0. Tìm mệnh đề đúng trong các mệnh đề sau.

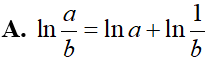
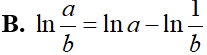
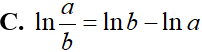
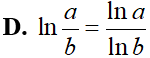
Cho a; b > 0 và  $a,b\ne 1$, x và y là hai số thực dương. Tìm mệnh đề đúng trong các mệnh đề sau:

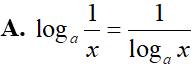
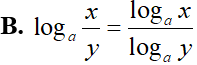
Cho hai số thực dương a, b với  $a\ne 1$. Khẳng định nào sau đây đúng?

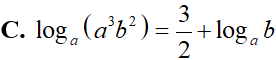
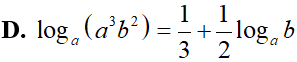
Với các số thực dương a, b bất kỳ. Mệnh đề nào dưới đây đúng?

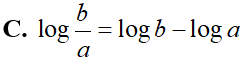
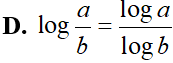
Cho a là số thực dương và b là số thực khác 0. Mệnh đề nào sau đây là mệnh đề đúng?

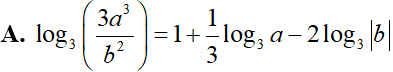
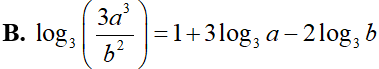
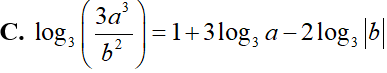
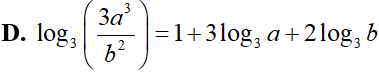
Cho a, b là các số thực dương khác 1. Mệnh đề nào sau đây sai?

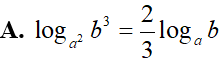
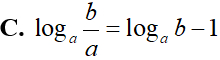
Cho hai số thực dương a và b, với a > b, (a – 1)(b – 1) > 0. Khẳng định nào dưới đây là khẳng định sai?

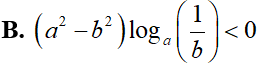
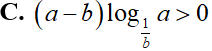
Cho hàm số y = f(x) thoả mãn điều kiện f(1) = 12, f^’(x) liên tục trên  $\mathrm{ℝ}$ và  ${\int }_1^4{f}^{\text{'}}\left(x\right)dx=17$. Khi đó f(4) bằng

Tính  $I={\int }_0^a{25}^{x}dx$ theo số thực a.

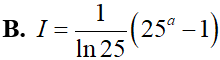
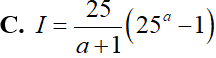
Biết F(x) là nguyên hàm của f(x) = 4^x và  $F\left(1\right)=\frac{3}{\ln 2}$. Khi đó giá trị của F(2) bằng.

Hàm số y = f(x) liên tục trên [2;9]. F(x) là một nguyên hàm của hàm số f(x) trên [2;9] và F(2) = 5; F(9) = 4. Mệnh đề nào sau đây đúng?