[2021] Trường THPT Liễn Sơn lần 3 - Đề thi thử THPT QG năm 2021 môn Toán Đề thi thử THPT Quốc gia môn Toán năm 2021 từ Trường THPT Liễn Sơn (lần 3), miễn phí với đáp án đầy đủ. Nội dung bao gồm các dạng bài cơ bản và nâng cao như giải tích, logarit, số phức và hình học không gian, giúp học sinh tự đánh giá năng lực và chuẩn bị tốt nhất cho kỳ thi Quốc gia.
Từ khoá: Toán học giải tích logarit số phức hình học không gian năm 2021 Trường THPT Liễn Sơn đề thi thử đề thi có đáp án
Bộ sưu tập: 📘 Tuyển Tập Bộ 500 Đề Thi Ôn Luyện Môn Toán THPT Quốc Gia Các Tỉnh Từ Năm 2018-2025 - Có Đáp Án Chi Tiết 📘 Tuyển Tập Đề Thi Tham Khảo Các Môn THPT Quốc Gia 2025 🎯
Bạn chưa làm đề thi này!
Bắt đầu làm bài
Câu 1:
Cho a , b a,b
A. ln ( a b 2 ) = ln a + ( ln b ) 2 . \ln \left( a{{b}^{2}} \right)=\ln a+{{\left( \ln b \right)}^{2}}. B. ln ( a b ) = ln a . ln b . \ln \left( ab \right)=\ln a.\ln b. C. ln ( a b 2 ) = ln a + 2 ln b . \ln \left( a{{b}^{2}} \right)=\ln a+2\ln b. D. ln a b = ln a ln b . \ln \frac{a}{b}=\frac{\ln a}{\ln b}.
Câu 2:
Cho hàm số y = f ( x ) y=f\left( x \right)
Câu 3:
Cho tập hợp A A A A
Câu 4:
Trong mặt phẳng tọa độ O x y , Oxy, M ( − 6 ; 1 ) M\left( -6;1 \right) O O k = 2 k=2
A. M ′ ( 12 ; − 2 ) . M'\left( 12;-2 \right). B. M ′ ( 1 ; − 6 ) . M'\left( 1;-6 \right). C. M ′ ( − 12 ; 2 ) . M'\left( -12;2 \right). D. M ′ ( − 6 ; 1 ) . M'\left( -6;1 \right).
Câu 5:
Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
B. y = log 2 3 x . y={{\log }_{\frac{2}{3}}}x. D. y = log 5 2 x . y={{\log }_{\frac{5}{2}}}x.
Câu 6:
Phương trình 1 − cos 2 x = 0 1-\cos 2x=0
A. { π 2 + k 2 π , k ∈ Z } . \left\{ \frac{\pi }{2}+k2\pi ,k\in \mathbb{Z} \right\}. B. { k 2 π , k ∈ Z } . \left\{ k2\pi ,k\in \mathbb{Z} \right\}. C. { π 4 + k π , k ∈ Z } . \left\{ \frac{\pi }{4}+k\pi ,k\in \mathbb{Z} \right\}. D. { k π , k ∈ Z } . \left\{ k\pi ,k\in \mathbb{Z} \right\}.
Câu 7:
Thể tích của khối chóp có diện tích đáy bằng 10 và độ dài chiều cao bằng 3 là
Câu 8:
Cho cấp số nhân ( u n ) \left( {{u}_{n}} \right) u 1 = 1 ; u 4 = 64. {{u}_{1}}=1;{{u}_{4}}=64. q q
Câu 9:
Tập xác định của hàm số y = ( x 2 − x ) − 3 y={{\left( {{x}^{2}}-x \right)}^{-3}}
A. R \ { 0 ; 1 } . \mathbb{R}\backslash \left\{ 0;1 \right\}. B. ( 0 ; 1 ) . \left( 0;1 \right). C. R \ { 0 } . \mathbb{R}\backslash \left\{ 0 \right\}. D. ( − ∞ ; 0 ) ∪ ( 1 ; + ∞ ) . \left( -\infty ;0 \right)\cup \left( 1;+\infty \right).
Câu 10:
Đồ thị hàm số nào sau đây có đường tiệm cận ngang?
D. y = x 2 − 2 x x − 1 . y=\frac{{{x}^{2}}-2x}{x-1}.
Câu 11:
Cho hình chóp tứ giác S . A B C D S.ABCD A B = a , S A ⊥ ( A B C D ) AB=a,SA\bot \left( ABCD \right) S A = a . SA=a. S . A B C D S.ABCD
Câu 12: A. Mỗi đỉnh của khối đa diện là đỉnh chung của ít nhất 3 mặt.
B. Hai mặt bất kỳ của khối đa diện luôn có ít nhất một đỉnh chung.
C. Mỗi mặt của đa diện có ít nhất 3 cạnh chung.
D. Mỗi cạnh của khối đa diện là cạnh chung của đúng 2 mặt của khối đa diện.
Câu 13:
Tập xác định của hàm số y = 3 − 2 x + 5 − 6 x y=\sqrt{3-2x}+\sqrt{5-6x}
A. [ 5 6 ; 3 2 ] . \left[ \frac{5}{6};\frac{3}{2} \right]. B. ( − ∞ ; 5 6 ] . \left( -\infty ;\frac{5}{6} \right]. C. [ 5 6 ; + ∞ ) . \left[ \frac{5}{6};+\infty \right). D. ( − ∞ ; 3 2 ] . \left( -\infty ;\frac{3}{2} \right].
Câu 14:
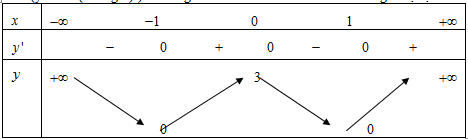
Khoảng nghịch biến của hàm số y = x 3 − 3 x + 3 y={{x}^{3}}-3x+3 ( a ; b ) \left( a;b \right) P = a 2 − 2 a b P={{a}^{2}}-2ab
Câu 15:
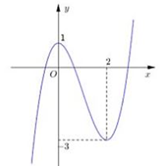
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A. y = x 3 − 3 x 2 + 1. y={{x}^{3}}-3{{x}^{2}}+1. B. y = x 3 − 3 x 2 . y={{x}^{3}}-3{{x}^{2}}. C. y = − x 3 + 3 x 2 + 1. y=-{{x}^{3}}+3{{x}^{2}}+1. D. y = x 3 + 3 x 2 + 1. y={{x}^{3}}+3{{x}^{2}}+1.
Câu 16:
Biết rằng phương trình log 3 ( x 2 − 2020 x ) = 2021 {{\log }_{3}}\left( {{x}^{2}}-2020x \right)=2021 x 1 , x 2 . {{x}_{1}},{{x}_{2}}. x 1 + x 2 . {{x}_{1}}+{{x}_{2}}.
A. x 1 + x 2 = 2020. {{x}_{1}}+{{x}_{2}}=2020. B. x 1 + x 2 = − 2020. {{x}_{1}}+{{x}_{2}}=-2020. C. x 1 + x 2 = − 2021 3 . {{x}_{1}}+{{x}_{2}}=-{{2021}^{3}}. D. x 1 + x 2 = − 3 2021 . {{x}_{1}}+{{x}_{2}}=-{{3}^{2021}}.
Câu 17:
Cho hàm số y = f ( x ) y=f\left( x \right) y = f ( x ) y=f\left( x \right)
Câu 18:
Phương trình log 2 2 x = log 2 x 4 2 \log _{2}^{2}x={{\log }_{2}}\frac{{{x}^{4}}}{2} a , b . a,b. a . b a.b
Câu 19:
Hàm số nào sau đây không có cực trị?
B. y = x 3 − 2 x 2 + 1. y={{x}^{3}}-2{{x}^{2}}+1. C. y = x − 1 3 x . y=\frac{x-1}{3x}. D. y = 2 x 4 + x 2 − 3. y=2{{x}^{4}}+{{x}^{2}}-3.
Câu 20:
Tìm hoành độ các giao điểm của đường thẳng y = 2 x − 13 4 y=2x-\frac{13}{4} y = x 2 − 1 x + 2 . y=\frac{{{x}^{2}}-1}{x+2}.
C. x = − 11 4 ; x = 2. x=-\frac{11}{4};x=2. D. x = 2 ± 2 2 . x=2\pm \frac{\sqrt{2}}{2}.
Câu 21:
Hàm số y = x 3 − 2 x , y={{x}^{3}}-2x, ( y C D ) \left( {{y}_{CD}} \right) ( y C T ) \left( {{y}_{CT}} \right)
A. y C T = − y C D . {{y}_{CT}}=-{{y}_{CD}}. B. y C T = 3 2 y C D . {{y}_{CT}}=\frac{3}{2}{{y}_{CD}}. C. y C T = 2 y C D . {{y}_{CT}}=2{{y}_{CD}}. D. 2 y C T = y C D . 2{{y}_{CT}}={{y}_{CD}}.
Câu 22:
Đạo hàm của hàm số y = 7 x 2 y={{7}^{{{x}^{2}}}}
B. y ′ = 7 x 2 . ln 7. y'={{7}^{{{x}^{2}}}}.\ln 7. C. y ′ = x .14 x 2 . ln 7. y'=x{{.14}^{{{x}^{2}}}}.\ln 7. D. y ′ = 2 x .7 x 2 . ln 7 y'=2x{{.7}^{{{x}^{2}}}}.\ln 7
Câu 23:
Cho lăng trụ đứng A B C . A ′ B ′ C ′ ABC.A'B'C' B , B B ′ = a B,BB'=a A C = a 2 . AC=a\sqrt{2}.
Câu 24:
Có bao nhiêu giá trị nguyên dương của m m y = x − 8 x − m y=\frac{x-8}{x-m}
Câu 25:
Giá trị nhỏ nhất của hàm số y = 2 x + 3 x + 1 y=\frac{2x+3}{x+1} [ 0 ; 4 ] \left[ 0;4 \right]
Câu 26:
Tìm giá trị của m m y = x 3 − x 2 + m x − 1 y={{x}^{3}}-{{x}^{2}}+mx-1
Câu 27:
Hàm số f ( x ) = log 3 ( 2 x + 1 ) f\left( x \right)={{\log }_{3}}\left( 2x+1 \right)
A. 2 ( 2 x + 1 ) ln 3 . \frac{2}{\left( 2x+1 \right)\ln 3}. B. 2 ln 3 2 x + 1 . \frac{2\ln 3}{2x+1}. C. 1 ( 2 x + 1 ) ln 3 . \frac{1}{\left( 2x+1 \right)\ln 3}. D. ln 3 2 x + 1 . \frac{\ln 3}{2x+1}.
Câu 28:
Phương trình 2 x 2 + x − 3 = 8 {{2}^{{{x}^{2}}+x-3}}=8 a , b . a,b. a + b a+b
Câu 29:
Cho hình chóp tam giác S . A B C , S.ABC, M , N M,N S B SB S C . SC. S . A M N S.AMN S . A B C S.ABC
Câu 30:
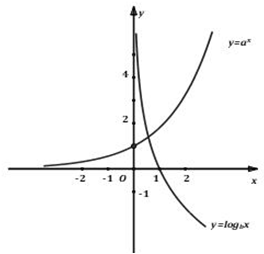
Cho đồ thị hai hàm số y = a x y={{a}^{x}} y = log b x y={{\log }_{b}}x
