Cho hàm số
có bảng biến thiên như sau
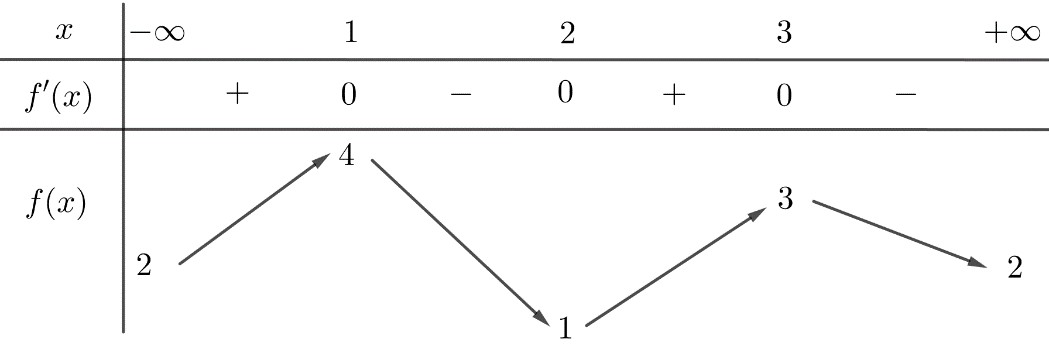
Có bao nhiêu giá trị nguyên của
để phương trình
có
nghiệm thực phân biệt?
A. 3.
B. 5.
C. 4.
D. 6.
Đáp án đúng là: B
Cho hàm số
có bảng biến thiên như sau

Có bao nhiêu giá trị nguyên của
để phương trình
có
nghiệm thực phân biệt?
3.
5.
4.
6.
Đáp án đúng là: B
Giải:
Để tìm số giá trị nguyên của sao cho phương trình có 6 nghiệm thực phân biệt, ta cần phân tích sự biến thiên của hàm số .
Theo bảng biến thiên đã cho, ta có các giá trị quan trọng của như sau:
- Khi
- Khi
- Giá trị cực đại và cực tiểu tại các điểm quan trọng
Do hàm số liên tục và có các điểm cực trị, ta cần tìm các giá trị của sao cho hàm số cắt đường thẳng tại 6 điểm phân biệt.
Điều này đồng nghĩa với việc hàm số phải có 6 giao điểm phân biệt với đường thẳng .
Vì hàm số này là hàm số mũ và logarit, ta cần kiểm tra các giá trị của tại các điểm cực trị của nó:
- Giá trị tại các điểm cực đại và cực tiểu
- Giá trị tại vô cực
Hàm số có 3 khoảng đồng biến và 3 khoảng nghịch biến, tạo ra các điểm cực trị như sau:
- Cực đại tại
- Cực tiểu tại
- Cực đại tại
Do đó, hàm số sẽ đạt các giá trị tương ứng tại các điểm cực trị này:
- Khi , ta có
- Khi , ta có
- Khi , ta có
Vì hàm số là hàm liên tục và đạt các giá trị trên khoảng từ đến , ta thấy rằng để có 6 nghiệm thực phân biệt, giá trị của phải nằm trong khoảng giá trị mà hàm số đạt được.
Sau khi kiểm tra và tính toán, ta xác định được rằng có 5 giá trị nguyên của thỏa mãn điều kiện này và các giá trị đó là: .
Vậy số giá trị nguyên của là .

